| 我的學系 |
國立臺灣大學 數學系 |
國立成功大學 數學系 |
|---|---|---|
| 所屬學群 |
數理化學群
數學學類 |
數理化學群
數學學類 |
| 所在校區 |
校本部 10617臺北市大安區羅斯福路四段1號 |
校本部 701 臺南市東區大學路1號 |
| 學系特色 |
本系歷經六十餘年教學研究與經營,培育了許多世界知名的數學家與統計學家,其中有十位為中央研究院院士。除了學術界之外,在其他領域亦有許多表現非常傑出的系友。為了延續並增長畢業系友在國內外傑出表現的成績,本系對於增聘教師、提昇學術風氣、改善教學環境以及培育學生不遺餘力,冀望藉由如此努力來提升臺大數學系在國際上的知名度,走出臺灣是我們追求的目標。 |
本系現有33位教師(教授16位、副教授15位、助理教授2位),分屬四個研究領域(分析與機統、代數與數論、幾何、計算與應數),是國內少數在代數、幾何、偏微分方程、機率統計及計算應用數學各領域均衡發展的系所。本系亦參考國內外一流大學的課程地圖,規劃完整的課程地圖及大學部與研究所合班開設的銜接課程,讓學生有紮實訓練的數學思維、也培養其相關應用領域的數學核心能力、並使其能掌握未來發展的方向。 |
| 學科意涵 |
數學探討數與形的結構,是一切科學與工程的語言與基礎。本系大學部的課程與訓練致力於培養學生的「基礎數學能力」,談論的對象既是數學理論研究的基本物件,又常是基礎科學與應用學科中處理許多問題極有威力的工具、許多現象的絕佳模型。 |
數學是人類最寶貴的資產,它不但是人類抽象思考的結晶,更是自然、工程 |
| 學習方法 |
未上傳圖片 修習基礎或進階的數學課程。主要是透過課程瞭解理論及其証明,並透過習題演練、與同儕及和教授的討論深化學習。 未上傳圖片 學生自組研討班閱讀專業書籍或論文。 未上傳圖片 找教授做學士論文,研究探討進階數學題材. |

抽象思考上包含分類、歸納、邏輯論証、與抽象符號運算及思維;實際操作則包含課堂講授、演習(習題)課、自主學習、及上機實作(科學計算相關課程需要將數值方法撰寫為程式執行,驗證演算結果與理論相符)。 圖解:抽象符號在課堂上的運用 版權:代數課-彭永寧教授 
課堂講授 圖解:課堂內容 版權:初等分析-史習偉教授 
演習(習題)課 圖解:助教微積分演習課 
自主學習 圖解:自主整理筆記 
上機實作:科學計算相關課程需要將數值方法撰寫為程式執行,驗證方法的性質與理論相符。 圖解:計算機概論與程式語言 版權:沈士育教授 |
| 高中階段可以準備的學習方法或方向 |
盡量修習高中學校開設的加深加廣課程,並利用我們系上的線上課程培養獨立學習的能力。 |
平時可以多思考各學習學科的框架與系統,並嘗試做系統性的分類與歸納,提升自己全面分析的思考能力。此外可以多閱讀數學相關期刊與書籍(例如:數學傳播或是高中數學競賽的相關叢書)、或瀏覽線上課程與短講,透過理解每個數學命題的構成、思考切入點、與每一解題步驟的理由與邏輯,來提升對數學的認知,同時也能讓自己的論證和抽象符號使用能力更為熟練。這些都是在學習大學數學上不可或缺的基礎能力。 |
| 與相關科系之異同 |
數學系以嚴格邏輯訓練為主要原則,在各個課程中展現不同的邏輯推演方式來解決真正自然的問題,對的事一定給證明而錯的事一定給反例,接受數學系訓練後的學生深受工商業界研發部門的喜愛。 |
數學系和理學院其他科系(物理、化學等等)都是基礎科學的研究,差別在於數學透過抽象化和邏輯推理的使用來解析並解決科學問題。本系一、二年級著重基礎數學訓練;三、四年級則著重應用數學與純數學之相輔相成,不強調兩者之分野。基於此理念,成大數學系的課程設計對於學生往應數與純數之發展,皆提供了足夠基礎訓練。 |
| 生涯發展容易誤解之處 |
以為讀數學系後,未來只能當數學老師或研究人員,殊不知數學系畢業生是業界研發部門的最愛,且轉唸研究所的領域也非常多元。請參考台大數學系數學沙龍網站有關數學系可能之生涯規劃。http://www.math.ntu.edu.tw/~salon/ |
數學系往往被認為畢業後很難找工作,常常被誤解為只能當數學老師。事實上很多學科,如物理、電機、資訊與數據科學,均與數學應用息息相關,所以很多數學系畢業生在相關領域都有不錯的發展。 |
| 學習方法容易誤解之處 |
低估數學的內容和抽象程度,所以在中學基礎學習時輕忽證明的訓練。 |
高中數學與大學數學非常不同。由於升學制度的關係,高中數學常常流於大量計算當中,讓人誤以為公式和計算技巧是最重要的,但在大學數學裡更看重想法和推導過程,而且課程密度也一下子被提升很多,如果沒有花足夠的時間很難完整地吸收理解。大一剛進來要能調整唸書的態度和方法。(請參考2-b回答。) |
| 學習資源或補充說明 |
數學系的課程都需要基礎,所以想要就讀的高中生一定要多修習加深加廣的相關課程。 |
如果附檔中之題目,你的答案是肯定的,你可能適合進數學系就讀。
|
| 我的學系 |
國立臺灣大學 數學系 |
國立成功大學 數學系 |
|---|---|---|
| 核心課程地圖 |
|
|
| 專業選修課程 |
|
|
| 特色課程 |
未上傳圖片 分析導論分析導論是微積分的延伸,一方面提供微積分中諸多概念更嚴格的論證基礎,另一方面也將這些概念推廣到更抽象的對象,比如說一些常用的函數空間。 未上傳圖片 線性代數基礎的線性代數探討向量空間(三度空間向量的推廣)的基本性質(基底、維度)與線性映射(它們的矩陣表達、秩、跡、核空間、行列式等基本性質、矩陣的抽象特性、各種特殊矩陣分解的抽象理解等等)。本系線性代數課程不限於矩陣的實際操作與數值計算,並強調抽象性質的理解與理論的建立,故能因應不同領域的應用。 未上傳圖片 幾何學導論研究平面上及空間中曲線的幾何性質,介紹曲率(彎曲程度)、扭率(非平面程度)以及 Frenet 標架 - 沿著曲線移動的一組特殊的基底向量,它反過來刻畫了該曲線在空間中的形狀。接著討論空間中曲面的幾何性質等,除了以上這些基礎概念,本課程還著重實例的計算。 未上傳圖片 代數導論透過解決五次多項式有沒有根式解這個重要數學問題的方法,介紹群環體三種抽象物件的定義和理論,透過此課程可以訓練修課同學的抽象思維和嚴格邏輯訓練! |
未上傳圖片 線性代數:這門課以線性方程及矩陣為開端,再逐一引進線性代數的基本概念,包括向量空間、線性變換、基底與維度、行列式、特徵值與特徵向量以及對角化。本門課是後續所有課程中的最基礎。 未上傳圖片 高等微積分:這是一個學年的課程。介紹微分、積分及函數性質,重點為定理的證明。我們研究實數系和其基本的拓撲結構,然後討論序列和級數。接下來我們討論函數的連續性、微分、與積分,並在最後推廣到談論函數所形成的序列和級數。本門課是所有分析相關理論的基礎。 未上傳圖片 代數學(一)、(二):代數學(一)及(二)延續線性代數課程,但其題材更為抽象,亦有更多證明的訓練。此課程中介紹群、環、體等結構,發展研究其結構的方法,並將其應用在不同領域中。本課程會持續地帶領學生深入了解數學,也增強學生以數學符號及口頭來溝通數學的能力,讓學生能優游自在地閱讀、了解數學、培養其對抽象數學的鑑賞能力。 未上傳圖片 幾何學(一):這門課的目的是研究曲線和曲面的幾何性質。我們將討論曲線的曲率和撓率、Frenet–Serret 公式、高斯映射、高斯曲率與均曲率、曲面的基本形式、測地線、Gauss–Bonnet 定理等課題。此課程已空間幾何的直觀,結合線性代數與微積分的基礎,帶領學生探索如何以計算來理解與呈現抽象的幾何性質。 未上傳圖片 科學計算導論:本課程介紹一些基礎科學計算工具,包括演算法與計算方法。此門課學習觀點就是”作中學”。除了老師講課之外,會提供現實問題的案例研究,引導學生通過實際操作來解決問題。課程內容如下: 函數計算、錯誤分析和複雜度計算 、密集/稀疏矩陣計算:矩陣分解、特徵值問題 、 求解線性和非線性方程的方法、數值優化。 |
| 完整課程地圖 |
| 我的學系 |
國立臺灣大學 數學系 |
國立成功大學 數學系 |
|---|---|---|
| 適合從事工作 |
|
|
| 系友生涯 |
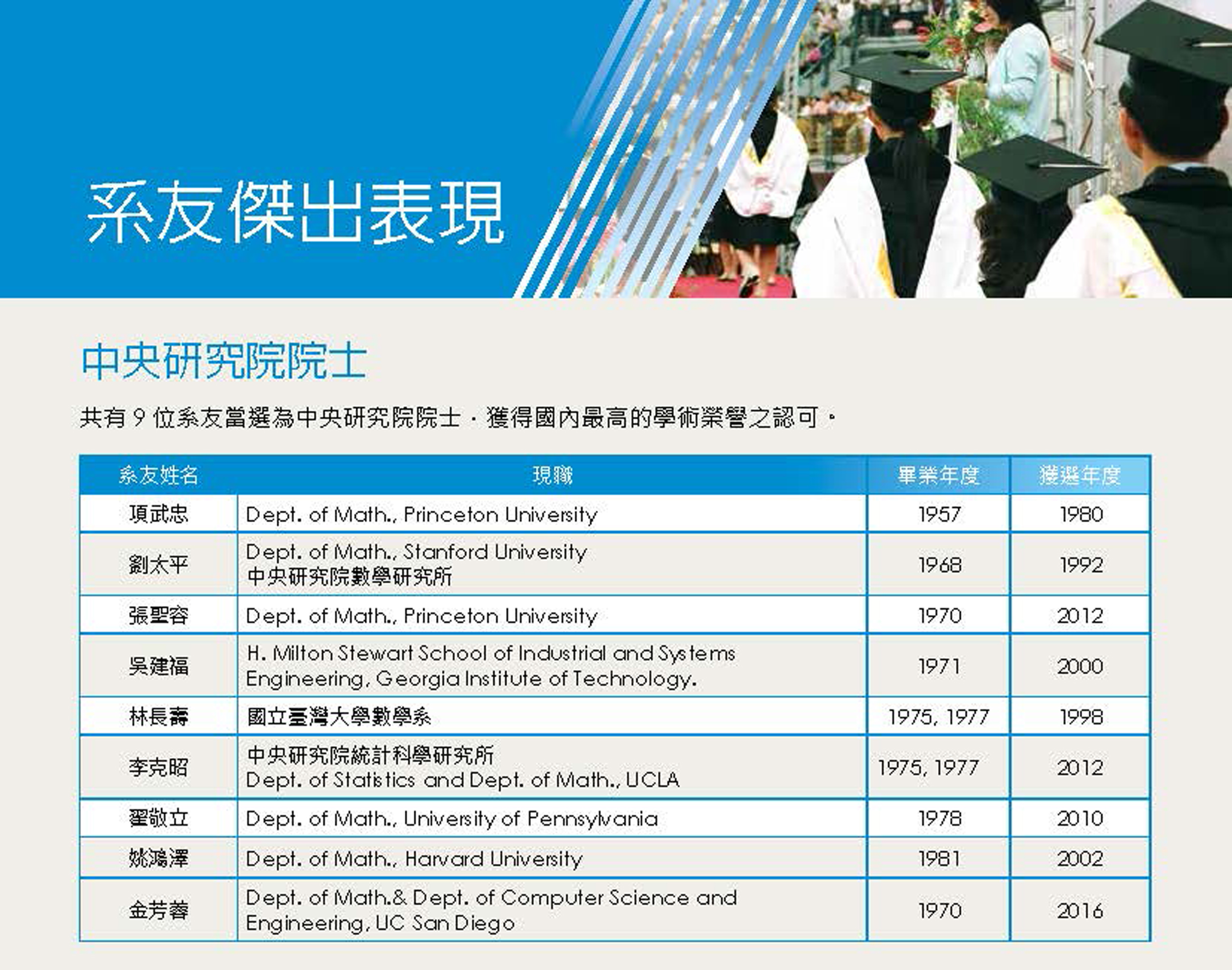
圖解:共有十位系友當選為中央研究院院士。 版權:數學系網頁
如圖如圖 如圖 
圖解:從事各行各業的傑出系友。 版權:數學系網頁
如圖如圖 如圖 
版權:數學系網頁
如圖如圖 如圖 |

圖解:目前研究領域為極端事件與尾部風險
林卲謙成功大學數學系;交通大學數學建模與科學計算所 大學時期所學是未來應用的基礎,在經濟、統計、機器學習(Machine Learning)、深度學習(Deep Learning)、演算法或是衍生性金融商品定價等領域都有不少的應用。研究所時期主要學習機率論與深度學習。 南山人壽 投資功能-資產配置部、投資服務部 量化研究員。 國泰投信 全球經濟與策略研究處 投資研究襄理。 工作內容主要使用量化方法建構投資策略、風險指標開發與績效歸因,其中會牽涉到演算法、機率模型及統計分析。
呂依帆 Yi-Fan Lu成大 105 級數學系;University of Manitoba 精算研究所 大二的時候有幸認識當時想走精算的學長,所以初次認識了精算這個行業,之後開始往統計精算的方面選課,也在大三暑假考過了第一科精算考試,正式走上精算的人生。 Canada Life Assurance Company ;ALM Actuarial Analyst 資產配置精算分析師。研究所畢業後有幸加入加拿大第二大的壽險公司,擔任資產配置的精算分析師,與團隊一起管理公司的各部門資產與負債。加拿大與其他西方國家有類似的職場文化,上下階級制度不明顯,對不同國家背景文化也有多元友善包容的職場倫理。 
張家齊1.成大數學系學士(2003-2007); 2.InnovoTech Labs資訊長(2012/12-2013/07);3.NumerInfo 共同創辦人(2013/09-2014/12) 4.Taiwan R User Group & MLDM Monday 共同創辦人(2012-) 張家齊目前是木刻思股份有限公司共同創辦人(2014-) ,是國內活躍的資料科學家,熱愛分析資料,建立模型,討論數學。於2012與同好開創 Taiwan R User Group 社群和 MLDM Monday 聚會。 |
我的學系 |
國立臺灣大學 數學系 |
國立成功大學 數學系 |
|---|---|---|
多元能力 |
邏輯推理:能捕捉事物運作的規律或關聯性,歸納或是推演不同事物的差異或因果關係,並得到特定理解。
20%
問題解決:分析並預判問題的成因與後果,設想出合適的解決方法及使用的工具。
10%
敏銳創造:能覺察特定事件與觀念、理論之間的差異,且能對事物進行拆解、組合、重新詮釋,呈現新穎之處。
10%
語文理解與表達:能透過語文理解他人想法形成特定概念,且能說明特定想法或因果關係。
5%
運作分析:分析特定需求並規劃合適的運作流程,運用技術調整、組裝、設定設備,讓設備及系統正常運作。
5%
程式設計:了解程式語法以及邏輯架構,撰寫、修改程式,開發並設計系統。
5%
系統運作:評估與分析系統的運作方式、效能,考慮運作成本與效益,制定系統運作可改善或調整的方式。
5%
數理科學:能選擇適當的科學、數理知識或邏輯來思考問題,依據科學規律正確地推演出答案或排列資訊。
5%
記憶詮釋:能識別、儲存、喚起多項資訊、數字、知識內容,且能以多種方式組合這些訊息間的差異與關聯。
5%
快速知覺與總結:能從散落的資訊中,快速分辨與覺察具有意義的訊息,且能歸納出要點、關聯、架構等概念。
5%
空間定向:能覺察環境、物體與自己的相對位置,辨別出方向、維度,想像物體在移動或重新排列後的外觀。
5%
專注力:投入心力在特定訊息及排除外部干擾。
5%
批判思考:運用不同觀點對問題進行理性分析,對問題的解決方法或結論,評估出優缺點、支持、反對的意見。
5%
主動學習:積極尋求新資訊用以掌握問題的前因、後果以及預期影響,並依據各環節選擇適合的學習行為。
5%
自省促進:收集、評估自己或他人的表現,提出可改善及調整的方法或採取行動。
5%
|
邏輯推理:能捕捉事物運作的規律或關聯性,歸納或是推演不同事物的差異或因果關係,並得到特定理解。
15%
數理科學:能選擇適當的科學、數理知識或邏輯來思考問題,依據科學規律正確地推演出答案或排列資訊。
15%
語文理解與表達:能透過語文理解他人想法形成特定概念,且能說明特定想法或因果關係。
10%
敏銳創造:能覺察特定事件與觀念、理論之間的差異,且能對事物進行拆解、組合、重新詮釋,呈現新穎之處。
10%
主動學習:積極尋求新資訊用以掌握問題的前因、後果以及預期影響,並依據各環節選擇適合的學習行為。
10%
問題解決:分析並預判問題的成因與後果,設想出合適的解決方法及使用的工具。
10%
自省促進:收集、評估自己或他人的表現,提出可改善及調整的方法或採取行動。
5%
記憶詮釋:能識別、儲存、喚起多項資訊、數字、知識內容,且能以多種方式組合這些訊息間的差異與關聯。
5%
快速知覺與總結:能從散落的資訊中,快速分辨與覺察具有意義的訊息,且能歸納出要點、關聯、架構等概念。
5%
空間定向:能覺察環境、物體與自己的相對位置,辨別出方向、維度,想像物體在移動或重新排列後的外觀。
5%
專注力:投入心力在特定訊息及排除外部干擾。
5%
批判思考:運用不同觀點對問題進行理性分析,對問題的解決方法或結論,評估出優缺點、支持、反對的意見。
5%
|
性格特質 |
深思力行:常常追求事物的條理秩序,審慎確認事物的彼此關係,行事仔細考量後果。
60%
變通開創:常常對多種事物,表達熱情興趣,對於既有事物,進行拆解、重組,給予新的理解與觀點,並且喜愛創造出令人意想不到的新事物。
20%
主動積極:常常主動提出特定見解,樂於付出活力與熱情投入特定問題、活動,引領他人的行動。
20%
|
堅毅負責:常常長時間專注投入於特定事物,排除干擾訊息,會對所承諾的事物,會負起責任目標、執行到底,享受追求成就。
15%
深思力行:常常追求事物的條理秩序,審慎確認事物的彼此關係,行事仔細考量後果。
15%
探究冒險:常常樂於探索未知事物、能夠容忍陌生情境,樂於把困難視為一種挑戰,在探索、挑戰未知中偏好看見自己的成長。
15%
變通開創:常常對多種事物,表達熱情興趣,對於既有事物,進行拆解、重組,給予新的理解與觀點,並且喜愛創造出令人意想不到的新事物。
15%
主動積極:常常主動提出特定見解,樂於付出活力與熱情投入特定問題、活動,引領他人的行動。
15%
自信肯定:總是相信自己能達成目標,會肯定自身的優勢、長處,面對挫敗能較好的調整情緒。
15%
開朗活潑:總是正向樂觀的看待事物的發展,即使事件發展不如預期,也能保持接納、能看見正向價值,常常表現自在、不膽怯。
10%
|
